Model and Implementation
We formalise the simplified game of Clue in a model. We implement this model digitally using Python. On this page, we will describe our model and implementation. The implementation itself can be found on our GitHub. It uses Mesa [2] and MLsolver [3].
- Formal card and player representation
- The Kripke Model
- Rules for gaining information
- Updating the Kripke model
- The implementation interface
Formal card and player representation
There are two different card categories: weapon and suspect. These are represented by the following sets:
- Weapons = {axe, candle, dagger, handgun, lead, rope, wrench}
- Suspects = {Scarlet, Mustard, Green, Plum}
Note that the cards in the weapon category are slightly different compared to the cards in the original Clue game. Instead of 'spanner', 'wrench' was used because the latter is a more well-known word for the same thing. 'candlestick' and 'lead pining' were shortened. 'revolver' was altered to the synonymous 'handgun'. This was done to ensure that all card names have a different first letter (which is useful when we want to use concise notations for them).
We will use the set \(\textrm{Cards} = \textrm{Weapons} \cup \textrm{Suspects}\) to refer to the set of all cards. There are three different players. We refer to them as 1, 2 and 3. That is, Players = {1, 2, 3}. The case file envelope is denoted by the singleton set Envelope = {\(\textrm{env}\)}
Each player or envelope might have a certain card, and therefore we will make use of the notation \(card_i\). Here, \( card \in \textrm{Cards} \) and \(i \in \textrm{Players} \cup \textrm{Envelope}\). An example is \(\textrm{revolver}_2\), meaning that player 2 has the revolver. In the example \(\textrm{Scarlet}_{\textrm{env}}\), Scarlet is the suspect that is in the case file envelope.
The Kripke Model
The Kripke model should represent the state combinations that include seven weapons, four suspects and three players. There is one weapon card and one suspect card in the envelope. This means that there are \(7 \times 4 = 28\) possibilities for the envelope. For the three players, there are nine cards left (weapons and suspects combined). Each player gets to have three cards. This leads to there being \(\frac{9!}{3! \times (9-3)!} = 84\) possible card combinations for player 1. When three of the nine cards are given to player 1, that leaves six cards for player 2. In effect, there are \(\frac{6!}{3! \times (6-3)!} = 20\) possible combinations for player 2. For player 3 there is only one option: they are left with the \(6 - 3 = 3\) remaining cards. In total, this all results in \(28 \times 84 \times 20 \times 1 = 47040\) states.
Each state contains one of the possible combinations of the 11 weapon and suspect cards. As an example, one such state is given by: axe\(_1\), candle\(_1\), dagger\(_1\), lead\(_2\), handgun\(_2\), rope\(_2\), Green\(_3\), Mustard\(_3\), Plum\(_3\), wrench\(_\textrm{env}\), Scarlet\(_\textrm{env}\). The envelope should contain one weapon and one suspect, but otherwise all cards are distributed randomly.
The Kripke model \(M = \langle S, \pi, R_1, R_2, R_3 \rangle\) can be defined as follows:
- \(S\) is the total set of states \(s = \{s_1, .., s_{47040}\}\). A state consists of a tuple of four pairwise disjoint sets: \(s = \langle c_{env}, c_1, c_2, c_3 \rangle \). The first of these sets denotes the cards in the envelope. The second, third and fourth sets denote the cards of players 1, 2 and 3 respectively. So, \(s = \langle \{card_{env}, card_{env}\}, \{card_1, card_1, card_1\}, \{card_2, card_2, card_2\}, \{card_3, card_3, card_3\} \rangle \).
- \(\pi : P \rightarrow (S \rightarrow \{T, F\})\) assigns a truth value to all propositions P for each state.
- \( R_1, R_2\) and \(R_3\) denote the set of relations for each player 1, 2 and 3. For each: \(R_j \subseteq S \times S\) such that \(R_j = \{(s, t) \in S \times S | c_j \textrm{ in } s \iff c_j \textrm{ in } t\}\), where \(j \in Players\). In other words, each player knows their own cards.
An visual depiction of (part of) a Kripke model is given in Example.
Rules for gaining information
In a game of clue, some logical rules apply. Players can use these rules to update their knowledge on the game. Using (a combination of) these rules, relations in \( R_1, R_2\) and \(R_3\) can be removed from the Kripke model. Note that for our model and implementation, we assume that the players are perfect logicians and can keep track of as much information as needed. In the real world, players often do not reason perfectly about the game and do not use these rules explicitly. The rules are:-
If one player has a certain card, then the other player cannot have that card.
If \(card_i\) with \(card \in \textrm{Cards}\) and \(i \in \textrm{Players} \cup \textrm{Envelope}\), then \(\neg card_j\) with \(j \in \textrm{Players} \cup \textrm{Envelope}\) and \(i \neq j\). That is, \(card_i \rightarrow \neg card_j\) for \(i \neq j\). - If each player has \(n\) cards and player \(i\) knows that player \(j\) has the set \(Cards_j\) with \(|Cards_j| = n\) (here, we use absolutes to denote the size), then if \(card \notin Cards_j\): \(\neg card_j\). Thus, \((card \notin Cards_j \textrm{ and } |Cards_j| = n) \rightarrow \neg card_j\).
-
If all except one of \(\textrm{Players} \cup \textrm{Envelope}\) does not have a certain card, then the
remaining player or envelope must have this card.
\(\neg card_i \textrm{ and } \neg card_j \textrm{ and } \neg card_k \rightarrow card_l\) with \(i, j, k, l \in \textrm{Players} \cup \textrm{Envelope}\) and \(i \neq j \neq k \neq l\). -
If for all except one weapon in \(Weapons\) or for all except one suspect in \(Suspects\),
you know that they belong to any player, then the remaining weapon or suspect is in the envelope.
If \( \textrm{ for each } card \in \textrm{Weapons} \backslash \{x\}\), \(card_j\) where \(j\ \in \textrm{Players}\), then \(x_{env}\).
If \(\textrm{ for each } card \in \textrm{Suspects} \backslash \{x\}\), \(card_j\) where \(j\ \in \textrm{Players}\), then \(x_{env}\).
Updating the Kripke model
As the players take turns, they gain more and more information. During a turn, a player \(i \in Players\) first makes a suggestion \(sug_i\). This suggestion should consist of one weapon and one suspect: \(sug_i = \{A, B\}\) such that \( A \in Weapons \) and \(B \in Suspects \).
The next player \(j\) gives a response \(res_{j}\). There are two options:
-
Player \(j\) does not have any of the cards suggested.
They share a public announcement:
\(\textrm{There does not exist a } card_{j} \textrm{ such that } card \in sug_i\). -
Player \(j\) does have one or both of the cards suggested.
They share a public announcement:
\(\textrm{There exists a } card_{j} \textrm{ such that } card \in sug_i\).
They pick one \(card_{j} \in sug_i\) and share a private announcement for player \(i\) only:
\(card_{j}\). (Note that here, \(card_{j}\) refers to a specific card, while in the public announcements, it refers to a variable).
Using the public and private announcements and the rules in Rules for gaining information, all players update their knowledge. For our model, this means that relations in the Kripke model are (potentially) removed. After all, based on a player's new knowledge, this player knows that some states might not be possible anymore. All relations pointing to these states are removed for the player. A detailed example is given in Example.
Public and private announcements can be seen as action models. Action models are of the structure \( \langle E, \sim, pre \rangle \) [4].
- \(E\) is a domain of action points or events
- \(\sim_a\) is an equivalence relation on \(E\)
- \(pre: E \rightarrow L \) is a precondition function that assigns a precondition to each \(e \in E\).
The precondition when showing a card is, for example, that the player has that card. In the detailed example of Example we will also discuss the relevant action models.
In our digital implementation, the Kripke model is indeed updated based on the players' newly gained information. Relations are removed iteratively after each player's turn. The rules described in Rules for gaining information are not explicitly stated in the implementation. Instead, these rules are elegantly, implicitly applied. This is because we only generate states for which the sets per player and envelope (\(c_{env}, c_2, c_3\) and \(c_4\)) are pairwise exclusive, for which these sets are of fixed lengths (two for the envelope, three for the players) and for which the envelope set always has one weapon and one suspect card. These limitations in the state generation makes it so that with little new information, a lot of relations can be directly removed. An example of this is given in Example.
If for any player \(j\), \(R_j \subseteq S \times S\) such that \(\textrm{ for all } R_j, R_j = \{(s, t) \in S \times S | c_{env} \textrm{ in } t\}\) (\(c_{env}\) is a constant here), they have won the game. In other words, if any player knows for sure what cards are in the envelope, they have won the game. In the Kripke model, this means that for this player \(j\), there are only relations \(R_j\) left that are all pointed towards a state with one certain envelope set \(c_{env}\). Note that this does not have to mean that there is only one relation left for a player. For instance, a player might not have yet found out whether one specific card belongs to player P or Q, but does know which cards are in the envelope.
In our implementation, after each player's turn, after the update of the Kripke model, the system goes through each player's relations in the Kripke model and checks, based on this, if there is a winner. The system then presents this winner and stops running. Notice that it might occur that there are multiple winners.
The implementation interface
The implementation is given as an interface. By running the implementation, a window pops up that shows:
- A table displaying the knowledge of the players. After each turn, the table is updated, giving the current information on what the players know. The information is displayed as following: Each column shows the information of one player. Notice that we use 'agent' instead of 'player' here, but the meaning is the same. The top row shows for each agent how many relations they still have in the Kripke model. The rows below show for each agent whether they know who owns the card of that row. For example, in the column 'Agent 1', row 'Mustard', the value there tells us whether Agent 1 knows where the card Mustard is. If this is a '?', this agent is not yet aware where that card is. If the value of a row is an Agent X, the column-agent knows that Agent X is in possession of that card.
- A button. Pressing it allows the model to give the next agent a turn.
- A message box, which tells you either what happened during the last turn or who is the winner.
An example of how the interface looks during a game is given below in Figure 1.
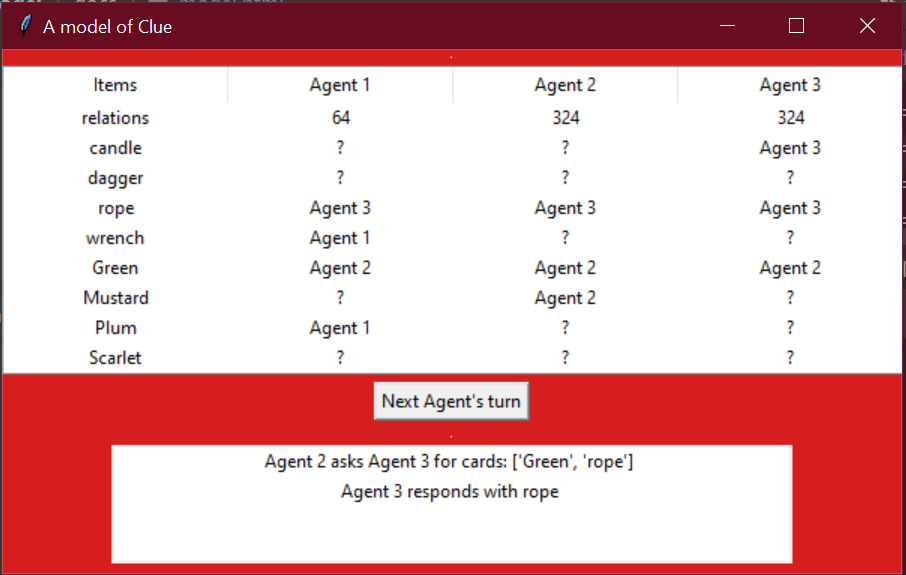
In this example, already a few turns are taken. From the message box we can see that during the last turn, Agent 2 asked Agent 3
whether they had any of the cards 'Green' and 'rope'. Agent 3 replied with 'rope'.
A private announcement is made to Agent 2 that agent 3 has 'rope'. Agent 2 now knows that Agent 3 has the card rope.
So, agent 1 knows that 'Green' or 'rope' was shown. Since Agent 1 already knew that
Agent 2 owns the Green card, they now know that Agent 3 has the rope card.
This can be seen in the table: The column of both Agent 1 and Agent 2 have 'Agent 3' in the rope column.
Note that sometimes during a turn the information in the table is not updated, but the relations are. This usually happens during the beginning of the game, when public announcements are made that tell us an agent has at least one of two cards. The agents cannot definitely tell that a certain agent has a certain card, but they can still cross off some states (namely, the states where the other agent does not have any of the two cards suggested).
For more information on how to run the implementation, read the README.md on Github